ZeroCho Blog

안녕하세요. 이번 시간에는 힙과 힙 정렬 대해 알아보겠습니다. 이 녀석은 트리이면서 배열인 이상한 놈입니다.

힙

힙은 트리의 일종이지만 조금 특이한 성질을 가지고 있습니다. 힙에는 최대힙과 최소힙이 있는데, 일단 최대힙의 정의는 다음과 같습니다. 

완전 트리이면서 Root가 모든 경우에 자식들보다 커야한다.

최소힙은 Root가 자식보다 작으면 됩니다. 완전 트리란 무엇일까요? 바로 노드가 순서대로 들어있는 트리가 완전 트리입니다. 왼쪽에서부터 차곡차곡 들어가는 트리죠. 한 줄이 다 찼으면 다음 줄 왼쪽에 노드가 들어가고요. 

Root가 자식보다 커야한다는 뜻은 다음과 같은 트리를 의미합니다. 트리 안의 서브트리에도 이 규칙이 적용됩니다. 또한 완전 트리이기 때문에 지난 시간처럼 트리로 만들지 않고 배열로 만들어도 됩니다. 다음 트리와 다음 배열은 같은 겁니다.

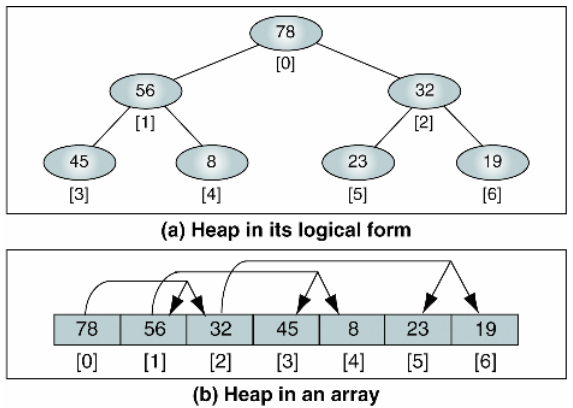
힙은 제거할 때 가장 위의 루트값이 빠집니다. 루트 값은 최대힙이면 숫자 중에 가장 큰 값, 최소힙이면 가장 작은 값이겠죠?

힙 정렬

위와 같은 힙의 성질을 이용해 힙 정렬을 할 수 있습니다. 랜덤한 순서의 숫자들을 힙으로 만들어 넣고, 힙에서 하나씩 제거하면 되죠. 가장 큰 값 또는 가장 작은 값 순서로 빠지기 때문에 알아서 정렬이 됩니다.

시간 복잡도는 데이터를 넣을 때도 O(lgN)이고 뺄 때도 O(lgN)이라 고른 성능을 보입니다. N개의 데이터를 모두 빼면 정렬이 되기 때문에 힙 정렬의 시간 복잡도는 O(NlgN)이 됩니다. 공간 복잡도는 O(n)입니다. 재밌게도 배열을 힙으로 만드는데는 O(nlg(n))이 아니라 O(n)의 시간 복잡도를 가집니다.

코드로 직접 만들어봅시다.

class MaxHeap { // 최대힙
    arr = []

    #reheapUp(index) {
        if (index > 0) {
            const parentIndex = Math.floor((index - 1) / 2);
            if (this.arr[index] > this.arr[parentIndex]) {
                // 값 바꾸기
                const temp = this.arr[index];
                this.arr[index] = this.arr[parentIndex];
                this.arr[parentIndex] = temp;
                this.#reheapUp(parentIndex);
            }
        }
    }
    insert(value) {
        const index = this.arr.length;
        this.arr[index] = value;
        this.#reheapUp(index);
    }
    #reheapDown(index) {
        const leftIndex = index * 2 + 1;
        if (leftIndex < this.arr.length) {
            const rightIndex = index * 2 + 2;
            const bigger = this.arr[leftIndex] > this.arr[rightIndex] ? leftIndex : rightIndex;
            if (this.arr[index] < this.arr[bigger]) {
                const temp = this.arr[index];
                this.arr[index] = this.arr[bigger];
                this.arr[bigger] = temp;
                this.#reheapDown(bigger);
            }
        }
    }
    remove() { // 루트 삭제
        if (this.arr.length === 0) {
            return false;
        }
        if (this.arr.length === 1) {
            return this.arr.pop();
        }
        const root = this.arr[0];
        this.arr[0] = this.arr.pop();
        this.#reheapDown(0);
        return root;
    }
    sort() { // 힙 정렬
        const sortedArray = [];
        while (this.arr.length > 0) {
            sortedArray.push(this.remove());
        }
        return sortedArray;
    }
    search(value) {
        for (let i = 0; i < this.arr.length; i++) {
            if (this.arr[i] === value) {
                return i;
            }
        }
        return null;
    }
    update(value, newValue) {
        const index = this.search(value);
        if (index === null) {
            return false;
        }
        this.arr[index] = newValue;
        for (let i = Math.floor(this.arr.length / 2 - 1); i >= 0; i--) { // O(1/2n)
            this.#heapify(i); // O(1)
        }
    }
    removeValue(value) { // 특정 값 삭제
        const index = this.search(value);
        if (index === null) {
            return false;
        }
        this.arr.splice(index, 1);
        for (let i = Math.floor(this.arr.length / 2 - 1); i >= 0; i--) { // O(1/2n)
            this.#heapify(i); // O(1)
        }
    }
    #heapify(index) {
        const leftIndex = index * 2 + 1;
        const rightIndex = index * 2 + 2;
        const bigger = (this.arr[leftIndex] || 0) > (this.arr[rightIndex] || 0)
            ? leftIndex : rightIndex;
        console.log(index, this.arr[index], this.arr[bigger]);
        if (this.arr[index] < this.arr[bigger]) {
            const temp = this.arr[index];
            this.arr[index] = this.arr[bigger];
            this.arr[bigger] = temp;
        }
    }
}

const heap = new MaxHeap();
heap.insert(5);
heap.insert(3);
heap.insert(7);
heap.insert(4);
heap.insert(2);
heap.insert(6);
heap.insert(1);
heap.sort(); // [7,6,5,4,3,2,1]

특이한 점은 reheapUp과 reheapDown이라는 내부적으로 힙의 순서를 재귀적으로 조정하는 함수가 있다는 겁니다. 힙은 트리를 배열로 표현한 것이기 때문에 트리 구조를 유지하려면 추가적인 과정 필요합니다. 

reheapUp은 배열 끝에 새로운 값을 받고, 그 값을 자신의 부모 노드(parseInt((idx - 1) / 2))와 비교해서 크면 서로 위치를 바꿉니다. 이를 재귀적으로 하면 됩니다. reheapDown은 배열 처음 값을 자기 왼쪽 자식(idx * 2 + 1), 오른쪽 자식(idx * 2 + 2) 둘 중에 큰 값과 비교해서 작으면 자리를 재귀적으로 바꿔줍니다.

sort 메소드를 호출할 시 내부적으로 delete를 this.arr의 개수만큼 호출합니다. 힙 정렬의 원리이죠? 최대값부터 빠지니까요. delete 메소드는 제일 첫 배열 값(빠지는 값)에 가장 마지막 배열 값을 넣고 reheapDown을 실행합니다.

heapify 함수는 heap이 아닌 이진트리를 힙으로 만드는 함수입니다. 생각보다 간단한게, leaf가 아닌 마지막 노드에서부터 루트까지 반복문을 돌면서 자식이 자신보다 크면 자신과 자리를 바꾸면 됩니다. 루트까지 반복문 돌고 나면 힙이 되어 있습니다. 이걸 활용해서 최대힙과 최소힙을 간단하게 전환할 수 있습니다.

힙은 정렬을 할 때 외에도 우선순위 큐를 만들 때에도 사용됩니다. 앞에서부터 요소가 빠지는 큐의 성질을 가지고 있고 항상 큰 값이 먼저 빠지기 때문입니다.

다음 시간에는 그래프에 대해 알아보겠습니다.