안녕하세요! 이번 시간에는 트리에 대해 알아보겠습니다!
이름이 트리인 이유는 나무처럼 생겼기 때문입니다. (정확히는 나무를 거꾸로 뒤집어놓았습니다.) 간단한 예로 HTML 구조가 있습니다. root(뿌리)부터 시작해서 아래로 가지치기를 합니다. 그래서 제일 마지막 노드는 뭐라고 부를까요? 바로 leaf(잎)입니다. 제일 위는 root고 제일 아래는 leaf니까 완전 나무를 거꾸로 뒤집어 놓은 거죠? root도 leaf도 아닌 노드들은 내부 노드라고 부릅니다.
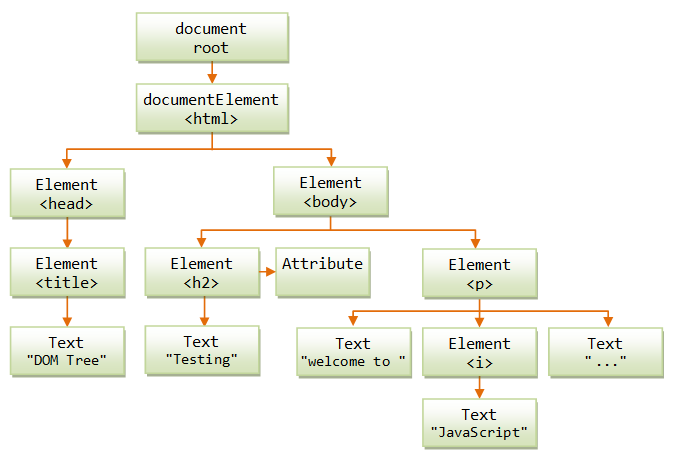
노드와 노드 사이를 이어주는 것은 branch나 edge라고 부릅니다. 시작점은 반드시 root 하나여야 합니다. HTML을 배웠으면 아시겠지만, 부모자식 관계, 형제자매 관계, 조상, 후손 등이 그대로 적용됩니다. 사실 HTML이 트리를 본딴 구조라서 그렇습니다.
그리고 위의 그림에서 document부터 마지막 Text까지 가는 길을 경로(path)라고 부릅니다. 그리고 부모노드에서 자식노드 사이의 edge 개수를 높이(height)라고 부릅니다. 예를 들면, 위의 경우에서 document root에서 Text "DOM Tree"까지의 높이는 4입니다. (화살표 4개를 거쳐왔기 때문)
트리에서 유의해야할 점은 트리의 아랫 부분도 모두 트리라는 겁니다. root가 없다고 생각해보세요. 그래도 트리죠? 또 Element<body>가 root라고 생각해보세요. 그것도 트리죠. 이렇게 트리 아래에 계속 트리가 나오기 때문에 재귀 함수가 사용됩니다.
실생활에도 트리는 엄청 많이 사용되는데요. 대진표, 지휘계통 등 단계나 계층이 있는 곳에서는 어김없이 사용됩니다. 그러니 트리에 대해 꼭 알아야겠죠? 그 중에서 우리는 자식을 최대 2개까지만 가질 수 있는 이진 트리에 대해 알아볼 겁니다. 또 우리는 이 시간에 이진 트리 중에서 이진 검색 트리에 대해 다룹니다. 왜 굳이 이진 검색 트리냐면, 중복 데이터가 없다는 가정 하에 크다와 작다를 쉽게 구분할 수 있기 때문입니다. 따라서 한 번 정렬하면 빠르게 찾을 수 있습니다. (O(lgn)) 사실 일반 트리도 모두 이진 트리로 변형할 수 있지만 그 방법은 여기서 다루지 않겠습니다.
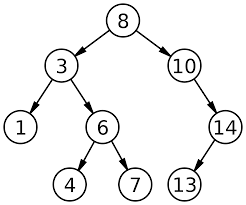
이진 검색 트리는 위와 같이 생겼습니다. 잘 보시면 숫자가 정렬된 것을 알 수 있습니다. 가장 작은 숫자는 가장 왼쪽에, 가장 큰 숫자는 가장 오른쪽에 있습니다. 코드로 만들어볼까요? 트리는 지금까지의 자료구조와 코드의 복잡성이 차원이 완전 다릅니다. 또한 트리를 만드는 방법에 주의하셔야합니다. 트리에 데이터를 넣을 때나 찾을 때, 제거할 때 대부분 재귀를 사용합니다. 그리고 자료구조에서 처음으로 비공개함수(private)가 사용되었습니다. 재귀 함수를 비공개함수 처리하여 재사용성을 높였습니다.
class Node {
left;
right;
constructor(data) {
this.data = data;
}
}class Tree {
count = 0;
root;
#insert(root, node) {
if (!root) return node;
if (node.data < root.data) {
root.left = this.#insert(root.left, node);
return root;
} else {
root.right = this.#insert(root.right, node);
return root;
}
return root;
}
add(data) {
const node = new Node(data);
if (this.count == 0) {
this.root = node;
} else {
this.#insert(this.root, node);
}
return ++this.count;
};
#get(data, node) {
if (node) {
if (data < node.data) {
return this.#get(data, node.left);
} else if (data > node.data) {
return this.#get(data, node.right);
} else {
return node;
}
} else {
return null;
}
}
get(data) {
if (this.root) {
return this.#get(data, this.root);
} else {
return null;
}
};
#remove(root, data) {
let newRoot, exchange, temp;
if (!root) return false;
if (data < root.data) {
root.left = this.#remove(root.left, data);
} else if (data > root.data) {
root.right = this.#remove(root.right, data);
} else {
if (!root.left) {
newRoot = root.right;
// root 메모리 정리
return newRoot;
} else if (!root.right) {
newRoot = root.left;
// root 메모리 정리
return newRoot;
} else {
exchange = root.left;
while (exchange.right) exchange = exchange.right;
temp = root.data;
root.data = exchange.data;
exchange.data = temp;
root.left = this.#remove(root.left, exchange.data);
}
}
return root;
}
remove(key) {
const node = this.#remove(this.root, key);
if (node) {
this.root = node;
this.count--;
if (this.count == 0) this.root = null;
}
return true;
};
}const tree = new Tree();
tree.add(5); // 1
tree.add(3); // 2
tree.add(4); // 3
tree.add(2); // 4
tree.add(7); // 5
tree.add(6); // 6
tree.root.left.data; // 3
tree.root.left.left.data; // 2
tree.root.left.right.data; // 4
tree;
tree.remove(3);
tree.root.left.data; // 2추가하는 것은 원하는 위치를 찾을 때까지 오른쪽 왼쪽 찾아가며 재귀를 통해 도달합니다. 찾는 것도 마찬가지죠. 지우는 게 문제입니다. 지우고자 하는 데이터를 재귀를 통해 찾아 지우면 되겠지만, 지운 후 트리가 이진 검색 트리 조건을 만족하는 지 확인해야 합니다.
따라서 지울 때 크게 세 가지 경우를 고려하게 됩니다.
- 왼쪽 자식 노드가 없을 때(숫자 10 노드처럼)
- 오른쪽 자식 노드만 없을 때(숫자 14 노드처럼)
- 그리고 왼쪽, 오른쪽 자식 노드 둘 다 있을 때(숫자 8)입니다.
양쪽 자식 노드가 모두 없을 때는 1. 왼쪽 노드가 없을 때와 같이 처리합니다(사실 그냥 노드를 뺀 것과 동일합니다).

왼쪽 자식 노드가 없다면(숫자 10의 경우) 오른쪽 노드를 끌어올려 지워진 공간을 채우면 되고, 오른쪽 자식 노드가 없다면(숫자 14의 경우) 왼쪽 노드를 끌어올리면 되는데요.
자식이 양쪽 다 있을 때(숫자 8의 경우)는 조금 다른 전략이 필요합니다. 일단 지우고자 하는 8 노드와 8의 왼쪽 자식 노드 중 가장 큰 노드(7)를 교환합니다. 그래야 이진 검색 트리 조건이 유지됩니다.

이제 7이 루트가 되고, 8은 7 자리로 교환되었습니다. 이후 3을 루트로 하는 트리에서 8을 지우면 됩니다. 현재 노드 8은 양쪽 자식이 모두 없으므로 1. 왼쪽 자식 노드가 없을 때의 조건에 해당합니다.

8을 지워버리면 새로운 이진 검색 트리가 완성됩니다. 이진 검색 트리의 삭제 기능은 노드의 자식 위치와 개수에 따라 분기 처리를 해주어야 해서 조금 더 복잡한 감이 있습니다.
이진 검색 트리의 공간 복잡도는 O(n)이고, 삽입, 검색, 삭제의 시간 복잡도는 O(lg(n))입니다. 다만 이는 이상적일 때일 뿐, 1-2-3-4-5-6같이 일직선인 모양의 트리가 되어버리면(1이 root, 6이 leaf) 시간 복잡도는 O(n)이 되어버립니다. 그래서 저런 일직선 모양의 트리가 되지 않게끔 하는 것이 AVL 트리나 레드블랙 트리입니다. AVL 트리는 뒤에서 배웁니다.
다음 시간에는 힙에 대해 알아보겠습니다!

네 여기서 반환해야 해서 필요합니다.